Data Types, scale and offset

Raster data types

• While R and Python have a variety of data types including character strings, raster data is always stored as numeric
• However, there are quite a number of numeric data types that can be used to store raster data, depending on the range of values and the precision required
• The choice of data type can have a significant impact on the size of the file and the precision of the data stored
• Since raster data is powered by GDAL, most raster based software (including R and Python) use the same data types when writing files to disk
  • In memory, only the datatypes supported by the programming languages are supported
• The numeric data types are supported by gdal are summarized in Table 7.1

Table 7.1: The possible ranges of different datatypes in gdal (source: Amatulli)

Data type	Minimum	Maximum	Size1	Factor
Byte	0	255	39M	1x
UInt16	0	65,535	78M	2x
Int16, CInt16	-32,768	32,767	78M	2x
UInt32	0	4,294,967,295	155M	~4x
Int32, CInt32	-2,147,483,648	2,147,483,647	155M	~4x
Float32, CFloat32	-3.4E38	3.4E38	155M	~4x
Float64, CFloat64	-1.79E308	1.79E308	309M	~8x

• If you store categorical data, use integer datatype and store the corespondence in the metadata
• Always be minimalistic about which datatype you need.
• Question if you have a continuous value from 0 to 1, which datatype do you use?
  • Not Float32! But Multiply by 100 and use Byte or by 1000 (if you need more precision) and use UInt16
• Question: if you are measuring temperature, and your values are floating point ranging is -20 to +40 degrees, what datatype are you going to use?
  • Not CFloat32!
  • Multiply by 100 and use CInt16
• Question: if you compute NDVI and have values in the range 0 - 1, what datatype do you use?
  • Not Float32, but not CInt16 either:
  • Transform the values to 0 - 255

Choosing a data type

• To minimize file size, it’s important to choose the data type that best fits the range of values in the raster
• At a first glance, it might seem that the numeric values we measured / calculated determine the datatype we use
• However, we can transform the values to a different range to fit a different datatype
• For example, if we have NDVI values ranging from -1 to 1, it might seem that we need to use CFloat32 to store these values. However, we can transform (rescale) these values to the range 0 - 255 and store them as Byte datatype.

Rescaling / Transforming values to 0 - 255

From Wikipedia:

To rescale a range between an arbitrary set of values [a, b], the formula becomes: \[x' = a + \frac{(x-min(x))\times(b - a)}{max(x)-min(x)}\]

For our usecase, we can consider:

• \(x'\) to be the stored value
• \(x\) to be the measured value
• \(a\) and \(b\) to be the maximum, minimum value of Byte (0 and 255 respectively)
• \(min(x)\) and \(max(x)\) the maximum and minimum measured values (-1 and 1 respectively)

We can use these values and simplify the formula as follows:

\[\begin{align} x' &= 0 + \frac{(x+1)\times 255}{2} \\ x' &= \frac{255x+255}{2} \\ x' &= 127.5x+127.5 \\ \end{align}\]

Rescaling NDVI values

• We can now use this formula \(x' = 127.5x+127.5\) to rescale NDVI values to the range 0 - 255
• So, rather than storing the NDVI value 0.2, for example, we store the value 153
• This rescaling is determined by two values:
  • scale and offset
  • \(x' = x \times \text{scale} + \text{offset}\)
  • In our NDVI example, scale is 127.5 and offset is 127.5 as well

Precision

Note that this transformation to 255 values limits our precision:

• Our values are now limited to in their precision, since we only have 255 possible values
• We can calculate the available precision like so: \(\frac{1}{\text{scale}}\)
• In our case this is \(\frac{1}{127.5} = 0.0078\).
• Any measured / calculated NDVI value will be rounded to a multiple of 0.0078.
• We need to decide if this precision is enough for our use case

R Implementation for vectors

• A generic way to implement this in R is as follows:

scale_minmax <- function(
    x, 
    a = 0,          # the minimum value of the new range (default 0)
    b = 255         # the maximum value of the new range (default 255)
    ){
  min_x = min(x) 
  max_x = max(x) 
  a + (x - min_x) * (b - a) / (max_x - min_x)
}

Take the following example:

# this creates 100 random NDVI values between -1 and 1
ndvi_measured <- runif(100, -1, 1)

ndvi_stored <- scale_minmax(ndvi_measured)

tibble(ndvi_measured, ndvi_stored) |>
  ggplot(aes(ndvi_measured, ndvi_stored)) + 
  geom_line(col = "grey") +
  geom_point() +
  labs(x = "Measured NDVI (-1 to +1)", y = "Stored value (0 to 255)") +
  theme_minimal()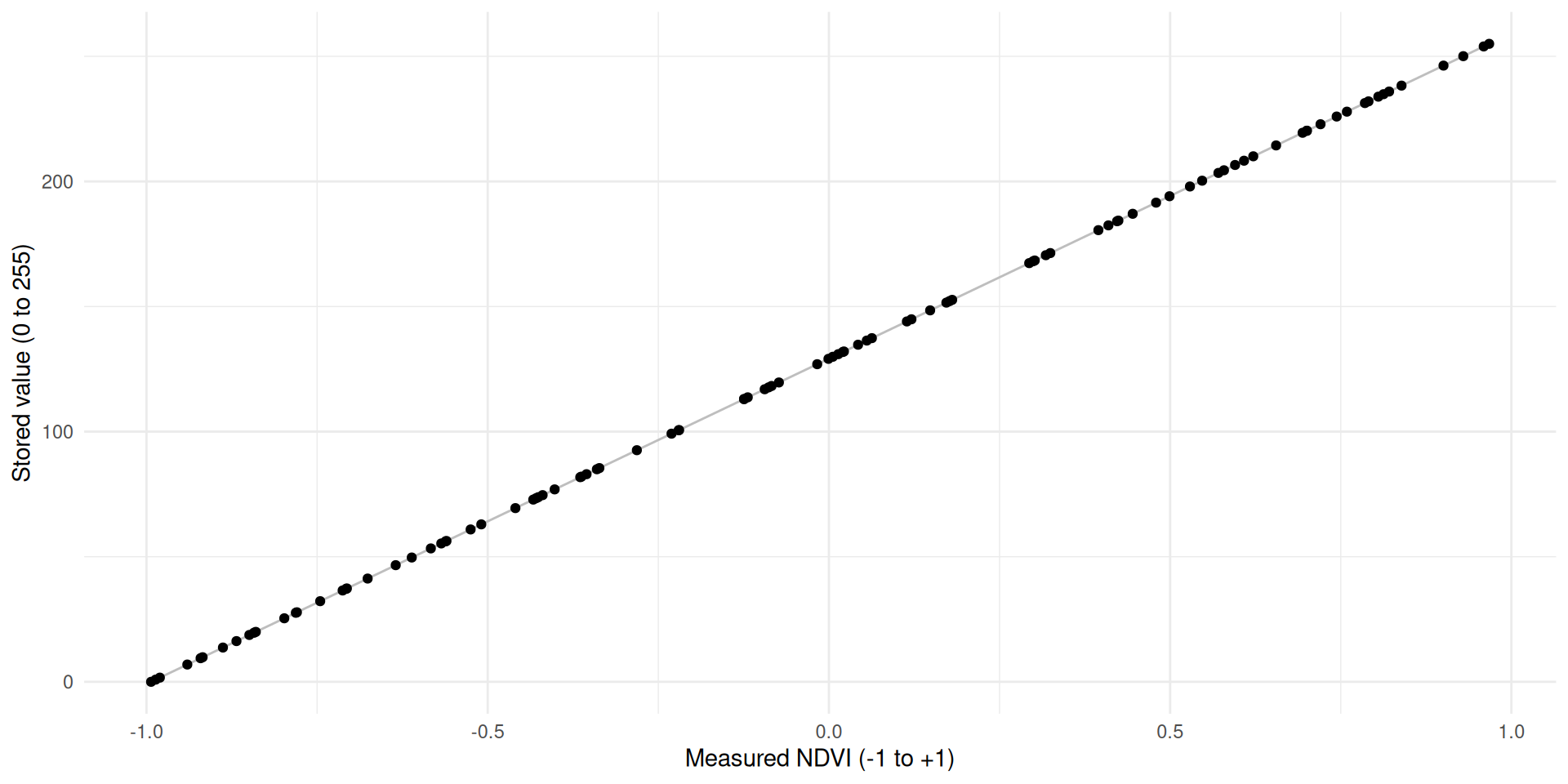

Restoring the original values

• Imagine you stored the NDVI values in the range 0 - 255, stored these values in a Geotiff and sent it to a colleague.
• To restore the original NDVI values the transformation (\(x' = 127x+127.5\)) needs to be known
• More precisely, the scale and offset values need to be known
• We can simply invert the transformation to get the original values back: \(x = \frac{x'-127.5}{127.5}\)

R implementation for rasters I

• Since rescaling values is a common operation, it is supported by GDAL and therefore most raster libraries
• Rather than transforming our values in memory, we can transform them when writing the raster to disk.
• For this, we can use the arguments scale = and offset = in the writeRaster function
• To use these arguments we need to calculate the scale and offset values first
• Rewriting the formula above, we can calculate scale and offset as follows:

\[\begin{align} \text{scale} &= \frac{b - a}{max(x)-min(x)} \\ \text{offset} &= \frac{a \times max(x) - b \times min(x)}{max(x)-min(x)} \end{align}\]

• To implement this in R, I use two functions: get_scale and get_offset:

get_scale <- function(
    x, 
    a = 0,          # the minimum value of the new range (default 0)
    b = 255,         # the maximum value of the new range (default 255)
    min_x = min(x),
    max_x = max(x) 
    ){
  
  scale <- (b - a) / (max_x - min_x)
  
  scale
}

get_offset <- function(
    x, 
    a = 0,          
    b = 255,
    min_x = min(x),
    max_x = max(x) 
    ){
  offset <- (a * max_x - b * min_x) / (max_x - min_x)
  
  offset
}


get_scale(ndvi_measured, min_x = -1, max_x = 1)

[1] 127.5

get_offset(ndvi_measured, min_x = -1, max_x = 1)

[1] 127.5

R implementation for rasters II

• The new functions get_scale(), get_offset() work nicely with vectors, but not with rasters
• The reason it does not work for raster is that min(x) (and max(x)) are local and not global functions
  • They return the minimum / maximum value per cell over all bands, not the global minimum / maximum value
  • To calculate the global minimum and maximum value, we can either use global, or the slightly faster minmax function
• Additionally, the writeRaster function will divide by scale and subtract offset from the values (see writeRaster), so we need to invert the two values
• This is how this is implemented in R:

get_scale2 <- function(
    x, 
    a = 0,          
    b = 255,
    min_max = minmax(x)[,1]
    ){
      library(terra)

      stopifnot(nlyr(x) == 1) # the function currently only works with 1 layer
      
      min_x <- min_max[1]
      max_x <- min_max[2]

      scale <- (b - a) / (max_x - min_x)
      
      1/scale           # invert the scale, since writeRaster divides by scale
}


get_offset2 <- function(
    x, 
    a = 0,          
    b = 255,
    min_max = minmax(x)[,1]
    ){
      library(terra) 

      stopifnot(nlyr(x) == 1) # the function currently only works with 1 layer

      min_x <- min_max[1]   
      max_x <- min_max[2]
      
      offset <- (a * max_x - b * min_x) / (max_x - min_x)
      
      offset * -1       # invert the offset, since writeRaster subtracts the offset
}

R implementation for rasters: example

• Let’s import a raster, calculate the scale and offset values and use these values to write to disk

library(terra)

elev <- rast(system.file("ex/elev.tif", package="terra"))

plot(elev, main = paste(minmax(elev),collapse = "-"))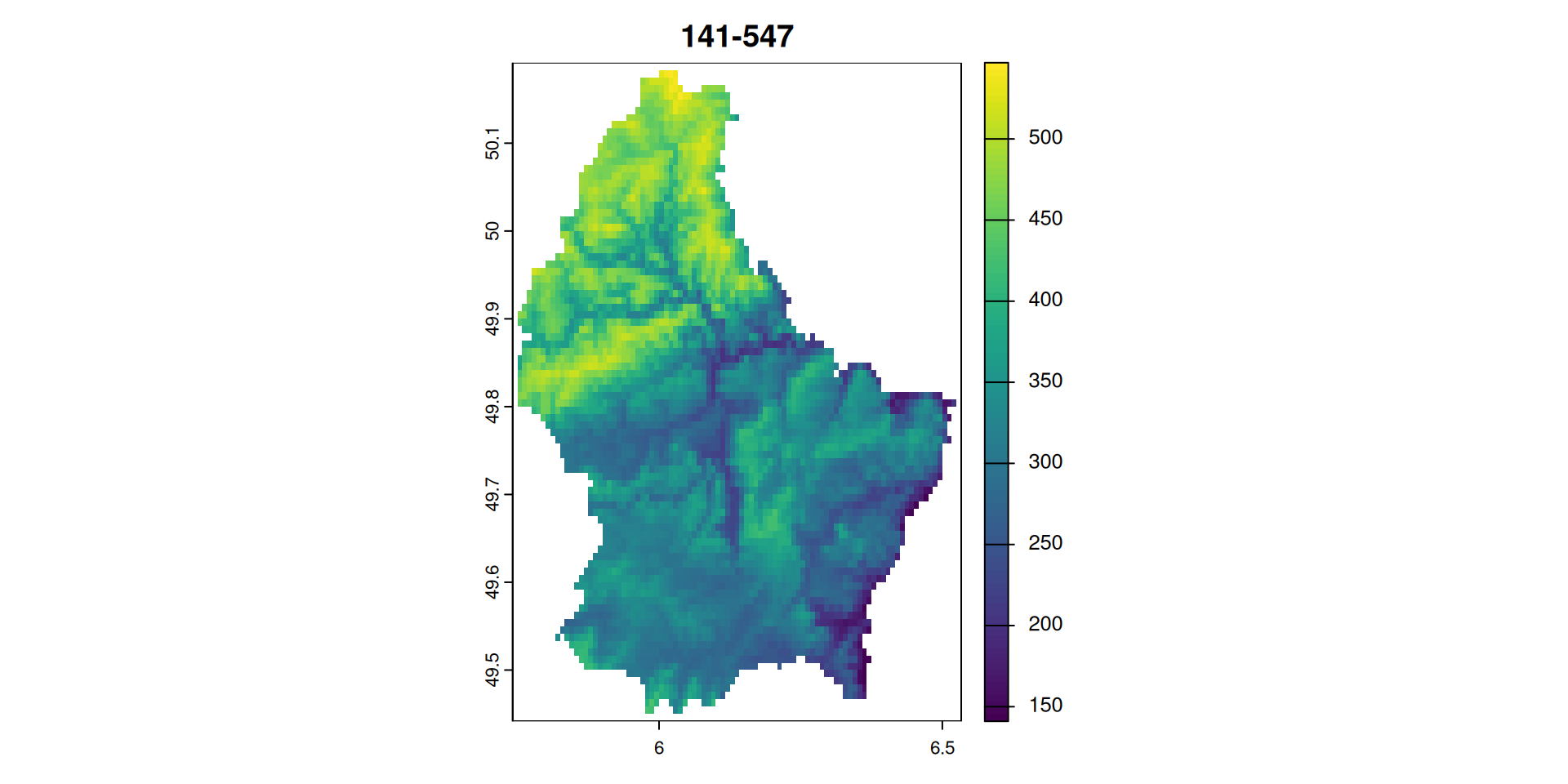

# write to disk with the minimum data type that fits the range 
# without transformation 

scale <- get_scale2(elev)
offset <- get_offset2(elev)

writeRaster(
  elev, 
  "data-out/datatypes/INT1U.tif",
  # datatype = "INT1U", 
  overwrite = TRUE, 
  scale = scale, 
  offset = offset
  )

R implementation for rasters: example

• Since GDAL stores the scale and offset values in the metadata, any software powered by GDAL will restore the original values on import
• In other words, if you run rast("data-out/datatypes/INT1U.tif") you will not notice the values were internally stored using 0 - 255. Instead, you will retrieve the original values.
• To finish off, let’s compare the file sizes of the raster stored as INT1U (Byte) and FLT8S (Float32)

writeRaster(
  elev, 
  "data-out/datatypes/FLT8S.tif",
  datatype = "FLT8S", 
  overwrite = TRUE
  )


filesize_INT1U <- file.size("data-out/datatypes/INT1U.tif")
filesize_FLT8S <- file.size("data-out/datatypes/FLT8S.tif")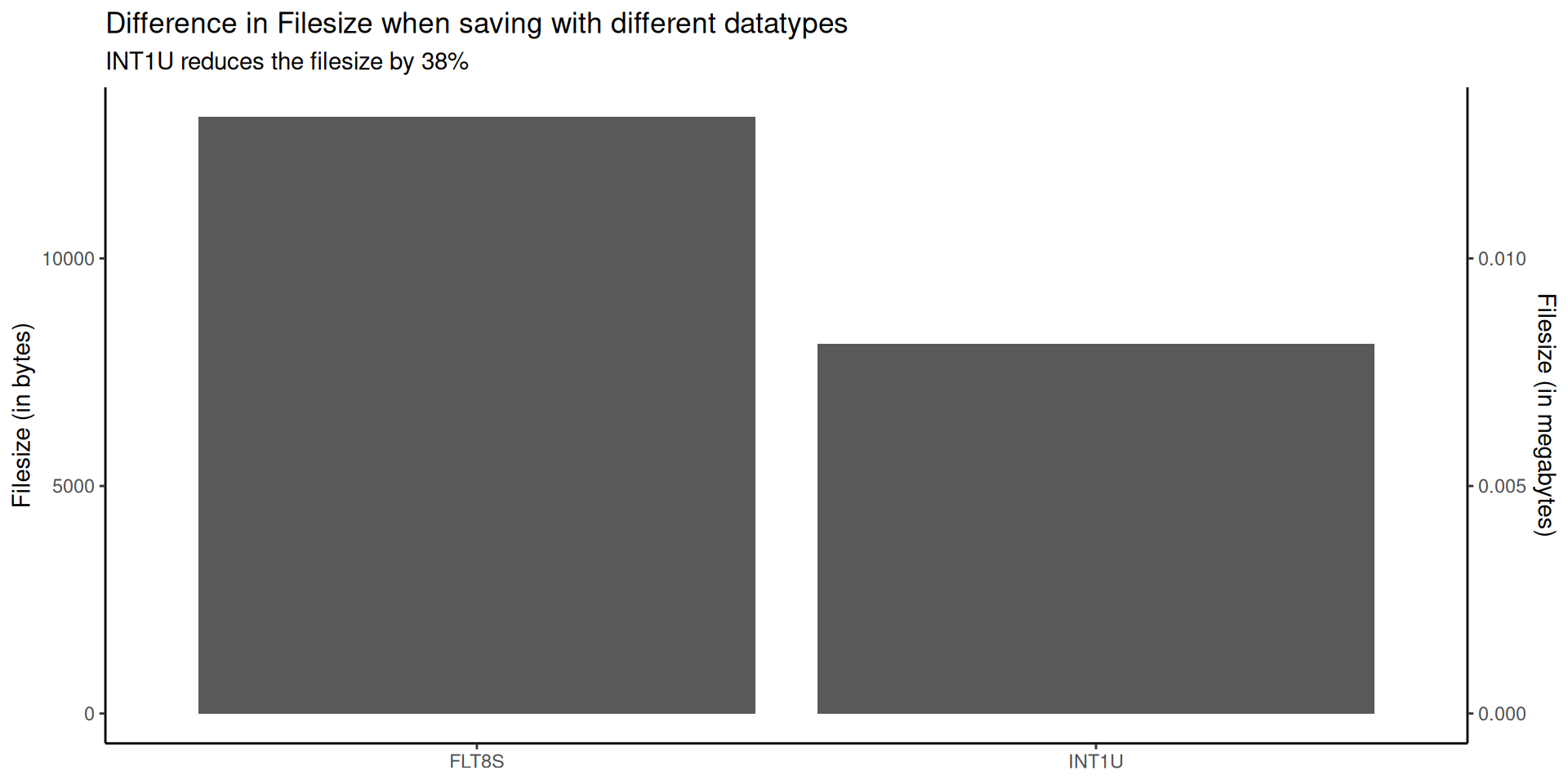

Amatulli, Giuseppe. “Geocomputation and Machine Learning for Environmental Applications.” http://spatial-ecology.net/docs/build/html/GDAL/gdal_osgeo.html.

---

1. Difference in file size using constant dataset (same values and resolution) and varying the datatype