Supervised Classification in Remote Sensing

Introduction

  • This lesson demonstrates supervised classification applied to remote sensing imagery
  • We’ll classify historic aerial imagery from 1961 to distinguish forest from non-forest areas in Ces, Ticino, Switzerland
  • Key focus: The spatial data workflow using terra/sf, not basic ML concepts

What makes RS classification different?

  • Spatial structure: Pixels are not independent - spatial autocorrelation matters
  • Scale of prediction: We predict on entire rasters (millions of pixels), not just point datasets
  • Spatial sampling: Ground truth comes from polygons, requiring careful sampling strategies
  • Feature engineering: Spatial context (focal operations) is critical, not just pixel values

These differences are why we can’t just apply generic ML tutorials to RS data!

The spatial workflow (terra/sf packages) and understanding spatial autocorrelation are essential skills, regardless of whether you use classical ML or deep learning.

Data

  • Historic aerial imagery from 1961 (swisstopo)
    • Single band (grayscale), 0.5 m/pixel resolution
    • Images available for: 1961, 1971, 1977, 1983, 1989, 1995
  • Ground truth forest polygons (hand-digitized)

Workflow Overview

  1. Load ground truth polygons and generate point samples
  2. Spatial train/test split (⚠ autocorrelation)
  3. Extract raster features using extract()
  4. Train classifier (CART for interpretability)
  5. Predict on entire raster
  6. Evaluate and compare approaches

Ground Truth & Spatial Sampling

From polygons to points

Unlike standard ML datasets, our ground truth comes as spatial polygons.

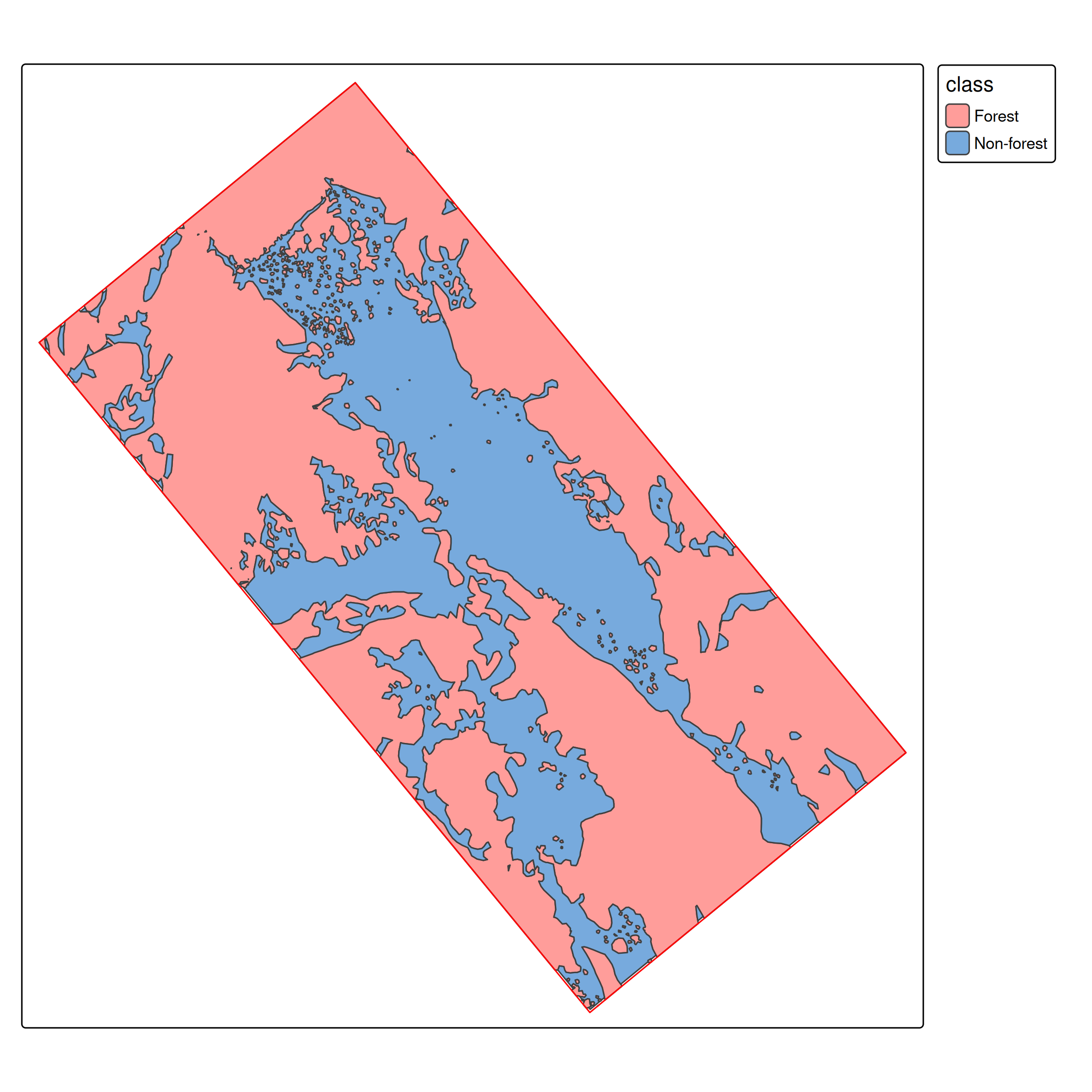
We need point samples for training:

# Load polygons
library(sf)
ces_polygons <- read_sf("data/ces_polygons.gpkg", "ces_polygons")
study_area <- read_sf("data/ces_polygons.gpkg", "study_area")

# Generate spatially distributed samples
sample_points <- st_sample(ces_polygons, 1000) |>
  st_sf()

# extract class per sample
labelled_data <- st_join(sample_points, ces_polygons) |>
  select(-jahr)

labelled_data$class <- factor(labelled_data$class)

Sample points from forest (green) and non-forest (orange) polygons

st_sample()

  • Ensures spatial coverage across polygon extents
  • Creates balanced datasets
  • Simple random sampling across the entire study region (more sophisticated strategies exist)

Train/test split: The spatial autocorrelation problem

Important

Spatial autocorrelation issue: Random splits violate independence assumptions because nearby pixels are correlated. Proper approaches use spatial cross-validation (Brenning 2023; Schratz et al. 2021). We use random splits here for simplicity, but be aware this may overestimate performance.

Pedagogical simplification: Random train/test split

Production approach: - Spatial k-fold cross-validation with geographic blocking - Ensures training and test data are spatially separated - Packages: sperrorest, mlr3spatiotempcv, CAST - More realistic performance estimates

Approach 1: Single-Band Classifier

Feature extraction with terra::extract()

train_features <- terra::extract(ces1961, data_train, ID = FALSE)

data_train2 <- cbind(data_train[,"class"], train_features) |>
  st_drop_geometry()

data_train2
       class luminosity
1 Non-forest  0.6352941
2     Forest  0.2078431
3     Forest  0.3960784
4     Forest  0.2980392
5     Forest  0.1294118
6 Non-forest  0.6980392

Training

We use CART (decision trees) for interpretability. As experienced ML practitioners, feel free to substitute with Random Forest, XGBoost, etc.

library(rpart)
cart_model <- rpart(class~luminosity, data = data_train2)

Pedagogical choice: CART for transparency

Production alternatives: - Random Forest / XGBoost: Better accuracy, handles non-linearity - Support Vector Machines: Good with limited training data - Neural Networks: Requires more data but state-of-the-art performance

CART lets students see exactly what decision boundaries the model learned.

Figure 10.1: Decision tree for single-band classification

Raster prediction

# Predict probability per class for all pixels
ces1961_predict <- predict(ces1961, cart_model)

# Get highest probability class
ces1961_predict2 <- which.max(ces1961_predict)

Classification result - single band approach

Evaluation

Table 10.1: Confusion matrix for single-band classification
Actual
Forest Non-forest
Forest 137 22
Non-forest 55 87

Overall accuracy: 0.74

The Spatial Context Problem

  • At pixel level, it is hard to distinguish forest from non-forest
  • Spatial context is essential: Humans use spatial context (texture, patterns, neighbors) to classify land cover
Figure 10.2

This is the core limitation of pixel-based classification.

Modern deep learning (CNNs) solves this automatically by processing image patches, but we’ll first show the manual approach to understand why spatial context matters.

Approach 2: Adding Spatial Features

  • Focal operations as feature extractors: Focal operations aggregate neighborhood values, providing spatial context
i <- 5
focal_window <- matrix(rep(1, i^2), nrow = i)

# Calculate standard deviation in each neighborhood
ces1961_focal_sd <- focal(ces1961, focal_window, fun = "sd")

Pedagogical approach: Handcrafted focal features

Why we do this: - Explicit, understandable feature engineering - Shows what spatial context means (texture/variation) - Works with classical ML algorithms

Production approach: Convolutional Neural Networks (CNNs) - CNNs learn optimal spatial filters automatically during training - First layer convolution weights = learned focal operations - Can learn multi-scale features (equivalent to multiple focal window sizes) - State-of-the-art: U-Net, DeepLabV3+, Vision Transformers

Original raster

After focal SD filter (shows texture/variation)
Figure 10.3

Normalization for multi-feature learning

When combining features, normalize to [0,1] using min-max scaling:

\[x' = \frac{x - \min(x)}{\max(x) - \min(x)}\]

minmax_normalization <- function(x){
  minmax_vals <- minmax(x)[,1]
  (x - minmax_vals[1]) / (minmax_vals[2] - minmax_vals[1])
}

ces1961_focal_sd <- minmax_normalization(ces1961_focal_sd)

# Combine original and focal features
ces_multi <- c(ces1961, ces1961_focal_sd)
names(ces_multi) <- c("luminosity", "focal_sd")

Training with spatial features

cart_model_multi <- rpart(class~., data = data_train2_multi)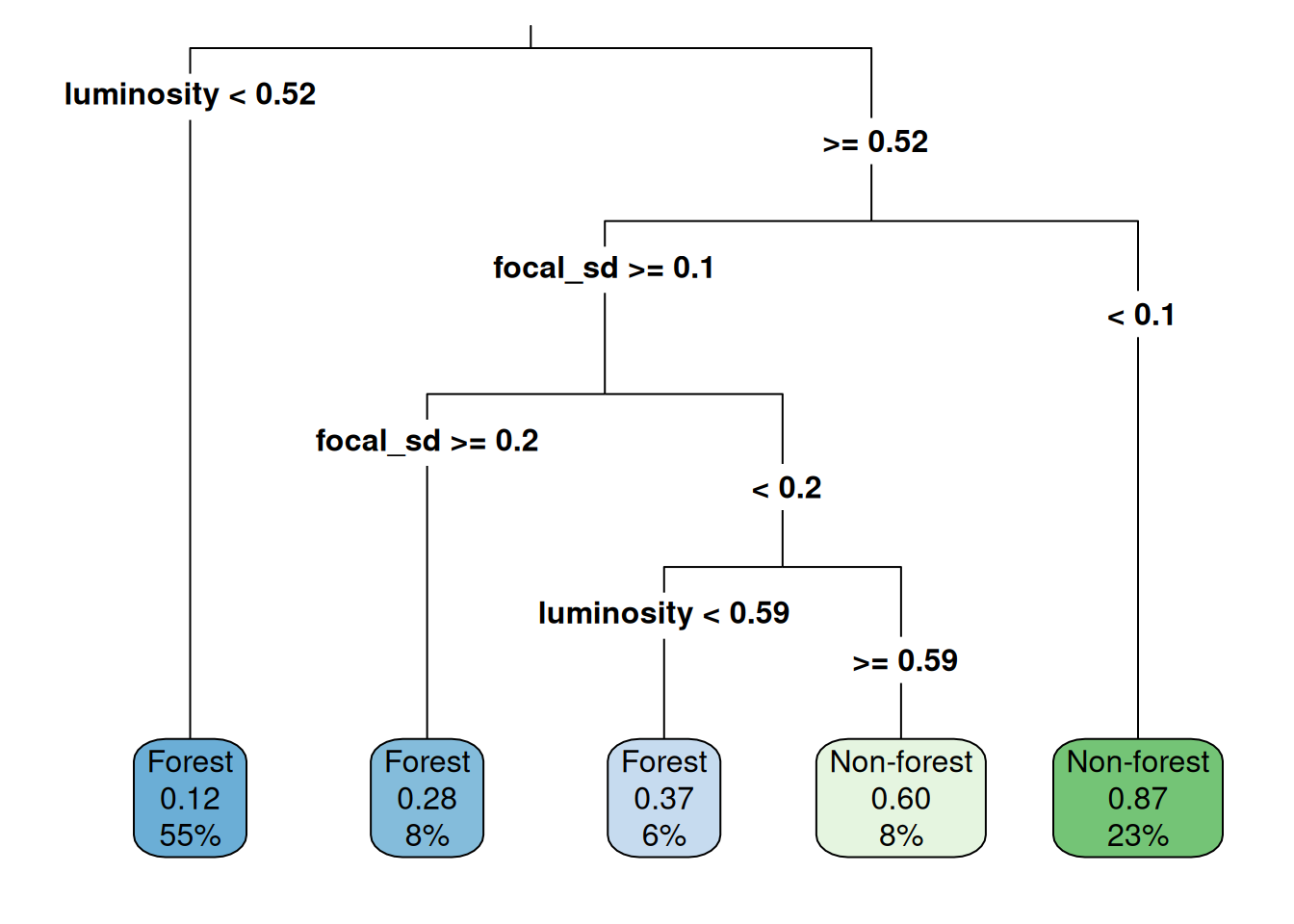
Figure 10.4: Decision tree now uses both luminosity and spatial texture

Prediction and evaluation

Table 10.2: Confusion matrix with spatial features
Actual
Forest Non-forest
Forest 175 37
Non-forest 17 72

Overall accuracy: 0.82 (vs. 0.74 without spatial features)

Further improvements

For advanced applications, consider:

  • More focal features: mean, variance, edge detection filters
  • Multi-scale features: focal operations at different window sizes
  • Deep learning: CNNs naturally capture spatial context
  • Object-based classification: segment first, then classify
  • Proper spatial CV: Use spatial blocking for more realistic evaluation

Key message for students:

Our approach teaches the concepts: - Why spatial context matters - How to work with spatial data in R - The ML workflow for remote sensing

In practice, you’d use deep learning frameworks (TensorFlow/PyTorch) with architectures designed for image segmentation. The concepts remain the same, but the implementation is more sophisticated.

Good starting points: - TorchGeo (PyTorch for geospatial data) - segmentation_models.pytorch (pre-built architectures) - Papers: U-Net for RS, DeepLabV3+, attention mechanisms

Tasks

Core exercises

  1. Download datasets (ces_polygons.gpkg and TIF files for 1961-1995) from Moodle
  2. Implement the complete workflow:
    • Load and sample spatial ground truth
    • Train classifier (single band or with additional features)
    • Evaluate with confusion matrix
  3. Apply model temporally and analyze forest cover trends